phân tích phương sai oneway anova, đây là phương pháp phân tích bằng phương sai tìm tìm khác biệt của quần thể mẫu thử, được thực hiện trên phần mềm R, với ví dụ cụ thể thực tế để cho các bạn dễ dàng áp dụng trong thực tiễn.
Như chúng ta đã biết kiểm định T-Test là tìm sự khác biệt trung bình của hai quần thể; bây giờ chúng ta đặt vấn đề là không phải 2 nhóm (quần thể) nữa mà là 3 nhóm hay 10 nhóm thì phương pháp T-Test có còn phù hợp nữa không ? Các bạn sẽ trả lời là chúng ta sẽ làm được bằng cách tách các cặp so sánh ra là, ví dụ như chúng ta có 10 nhóm thì C210 /2 cách chọn cách bắt cặp; Giữa sử chúng ta không phải là có 10 nhóm mà là có 100 nhóm thì … vẫn làm được nhưng rất cực và lâu.
Khi chúng ta bắt cặp ra thì kết quả có thể đúng nhưng sai hoàn toàn về phương pháp làm, nó dẫn đến kết quả sai lệch; bởi vậy phương pháp anova oneway ra đời để khắc phục giả thuyết trên. Tức là phân tích phương sai oneway anova là tìm sự khác biệt của nhiều nhóm khác nhau.
Phân tích phương sai oneway anova là gì ?
Trong thống kê , một chiều phân tích phương sai (viết tắt một chiều ANOVA ) là một kỹ thuật có thể được sử dụng để so sánh phương tiện của hai hay nhiều mẫu (bằng cách sử dụng phân phối F ). Kỹ thuật này chỉ có thể được sử dụng cho dữ liệu phản hồi số, “Y”, thường là một biến và dữ liệu đầu vào phân loại bằng số hoặc (thường), “X”, luôn luôn là một biến, do đó “một chiều”.
ANOVA kiểm tra giả thuyết khống rằng các mẫu trong tất cả các nhóm được rút ra từ các quần thể có cùng giá trị trung bình. Để làm điều này, hai ước tính được thực hiện của phương sai dân số. Những ước tính này dựa trên các giả định khác nhau ( xem bên dưới ). ANOVA tạo ra một thống kê F, tỷ lệ phương sai được tính giữa các phương tiện với phương sai trong các mẫu. Nếu phương tiện nhóm được rút ra từ các quần thể có cùng giá trị trung bình, phương sai giữa các phương tiện nhóm phải thấp hơn phương sai của các mẫu, theo định lý giới hạn trung tâm . Do đó, tỷ lệ cao hơn ngụ ý rằng các mẫu được rút ra từ các quần thể có giá trị trung bình khác nhau.
Tuy nhiên, thông thường, ANOVA một chiều được sử dụng để kiểm tra sự khác biệt giữa ít nhất ba nhóm, vì trường hợp hai nhóm có thể được bao phủ bởi phép thử t (Gosset, 1908). Khi chỉ có hai phương tiện để so sánh, các t-test và F-test là tương đương; mối quan hệ giữa ANOVA và t được cho bởi F = t 2 . Một phần mở rộng của ANOVA một chiều là phân tích phương sai hai chiều , xem xét ảnh hưởng của hai biến độc lập phân loại khác nhau trên một biến phụ thuộc.
Ví dụ ứng dụng phân tích phương sai
Chúng ta có một trang trại gà lên tới vài trăm ngàn con, Chúng tôi nhập khẩu 3 công nghệ nuôi mới tạm gọi là Phương án A + Phương án B + Phương án C; Làm thế nào mà chúng tôi biết cộng nghệ chăn nuôi nào tốt nhất để áp dụng cho trang trại chúng tôi.
Chúng tôi lựa chọn ra 200 con gà và cho chúng áp dụng với 3 công nghệ nuôi; với các điều kiện khác không đổi chỉ khác công nghệ nuôi, với tần suất áp dụng vật nuôi trong công nghệ như sau:
summary(factor(PP))
1 2 3
67 46 87
- Với phương án A: 67 con
- Phương án B: 46 con
- Phương án C: 87 con
Sau thời gian ba tháng chúng ta đem cân lại thì được trọng lương như biến CanNang
CanNang
n missing distinct Info Mean Gmd .05 .10
200 0 200 1 2.56 0.9163 1.367 1.509
.25 .50 .75 .90 .95
1.969 2.451 3.076 3.755 4.014
lowest : 1.021877 1.148578 1.152670 1.250324 1.254596
highest: 4.319929 4.599658 4.653071 4.730016 4.966406
Bây giờ chúng ta mới đặt ra câu hỏi là có sự hiệu quả khi áp dụng công nghệ mới không ? Hay nói theo thống kê là có sự khác biệt trong 3 công nghệ không ?
Phân tích phương sai oneway anova
Phân tích bằng biểu đồ
Trước khi dùng kết quả ước lượng để phân tích, chúng ta nhìn qua biểu đồ boxplot cũng cho ta thấy được phần nào kết quả kiểm định phương sai anova sắp diễn ra.
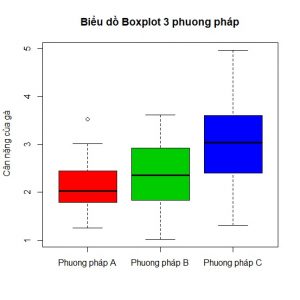
Từ biểu đồ trên thì chúng ta dễ dàng nhận thấy rằng, giữa phương pháp A và B có sự khác biệt không đáng kể, nhưng với phương pháp A với C thì có sự khác biệt lớn, hay cũng có sự khác biệt giữa phương án B với C; Với phân tích phương sai anova thì biểu đồ boxplot là một trong những biểu đồ quan trọng, mà nó cho chúng ta thấy được ” diễn cảnh phía trước”.
Phân tích phương sai trên phần mềm
Chạy phân tích phương sai trên phần mềm thống kê R chúng ta có kết quả như sau:
Df Sum Sq MeanSq F value Pr(>F)
PP 1 31.48 31.481 62.55 1.79e-13 ***
Residuals 198 99.65 0.503
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Ta đặt giả thuyết như sau:
- H0: Không có sự khác biệt giữa các nhóm trên
- H1: Có sự khác biệt giữa các nhóm
Ta có Pvalue < 0.05, ta bác bỏ H0 chấp nhận H1; Tức là có sự khác biệt giữa các nhóm; Hay nói cách khác là có áp dụng công nghệ nuôi gà mới có hiệu quả.
Như vậy thì chúng ta chọn phương án nuôi gà nào ? Nhìn bào biểu đồ thì ta dễ dàng nhận thấy rằng phương pháp C là tốt nhất, Giờ thì chúng ta cần kiểm định lại điều này xem nó có chính xác không ?
Kiểm định hậu định poct-hoc anova
Đây là kiểm định cần thiết của sự khác biệt từng cặp trong phân tích phương sai
> TukeyHSD(anova)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = CanNang ~ factor(PP))
$`factor(PP)`
diff lwr upr p adj
2-1 0.2525717 -0.06682941 0.5719729 0.1509220
3-1 0.8982920 0.62716240 1.1694215 0.0000000
3-2 0.6457202 0.34163114 0.9498093 0.0000035
Từ kết quả của kiểm định Tukey chúng ta có:
- Không có sự khác biệt giữa phương án A và B
- Có sự khác biệt giữa phương án B và C
- Có sự khác biệt giữa phương án A và C
Kết luận kiểm định phương sai anova
Sau khi kiểm định tukey và biểu đồ thì chúng ta dễ dàng nhận thấy rằng, phương án C là phương án tối ưu. Tức là áp dụng công nghệ của phương án C vào nuôi gà, thì làm cho năng suất ( cân nặng) của gà tăng cao.
Trên đây là chúng tôi hướng dẫn các bạn áp dụng phân tích phương sai vào một ví dụ cụ thể,nếu các bạn có nhu cầu lên phương án thực tế, hay nghiên cứu định lượng, hướng dẫn chạy mô hình định lượng … các bạn đừng ngần ngại hãy liên hệ ngay với chúng tôi, để được chúng tôi tư vấn và báo giá.
Chân thành cảm ơn !