hồi quy ridge ước lượng lasso tính elastic, đây là phương pháp hồi quy mới dùng để ước lượng các vấn đề mà phương pháp hồi quy tuyến tính không làm được, chúng ta dùng phương pháp phi tuyến được ước lượng lasso hồi quy ridge tính elastic … chúng tôi thực hiện 3 mô hình định lượng này trên phần mềm thống kê R; Nhằm giúp các bạn có cái nhìn thấu đáo và rõ ràng về các ước lượng phi tuyến này.
Hồi quy Ridge là gì ?
Hồi quy Ridge là một kỹ thuật để phân tích nhiều dữ liệu hồi quy chịu sự đa hình. Khi đa cộng tuyến xảy ra, ước tính bình phương tối thiểu là không thiên vị, nhưng phương sai của chúng lớn nên chúng có thể cách xa giá trị thực. Bằng cách thêm một mức độ sai lệch cho các ước tính hồi quy, hồi quy sườn giúp giảm các lỗi tiêu chuẩn.
Hy vọng rằng hiệu ứng ròng sẽ mang lại những ước tính đáng tin cậy hơn. Một kỹ thuật hồi quy thiên vị khác, hồi quy thành phần chính, cũng có sẵn trong NCSS. Hồi quy Ridge là phổ biến hơn trong hai phương pháp.
Ước lượng Lasso là gì ?
Trong thống kê và học máy , lasso ( toán tử co ngót và chọn lọc tối thiểu tuyệt đối ; Lasso hoặc LASSO) là một phương pháp phân tích hồi quy thực hiện cả lựa chọn và chính quy hóa để tăng cường độ chính xác dự đoán và khả năng diễn giải của mô hình thống kê mà nó tạo ra. Ban đầu nó được giới thiệu trong văn học địa vật lý vào năm 1986, và sau đó được tái phát hiện và phổ biến một cách độc lập vào năm 1996 bởi Robert Tibshirani , người đã đặt ra thuật ngữ này và cung cấp những hiểu biết sâu sắc hơn về hiệu suất quan sát được.
Lasso ban đầu được xây dựng cho các mô hình bình phương tối thiểu và trường hợp đơn giản này cho thấy một số lượng đáng kể về hành vi của công cụ ước tính, bao gồm mối quan hệ của nó với hồi quy sườn và lựa chọn tập hợp con tốt nhất và các kết nối giữa ước lượng hệ số Lasso và được gọi là ngưỡng mềm. Nó cũng tiết lộ rằng (như hồi quy tuyến tính tiêu chuẩn ) các ước tính hệ số không cần phải là duy nhất nếu các hiệp phương sai được cộng tuyến .
Mặc dù ban đầu được xác định cho các phương nhỏ nhất, quy tắc Lasso có thể dễ dàng mở rộng đến một loạt các mô hình thống kê bao gồm khái quát hóa tuyến tính mô hình , khái quát hóa ước lượng phương trình , những mối nguy hiểm mô hình tỷ lệ , và M-ước lượng , trong một thời trang đơn giản. Khả năng thực hiện lựa chọn tập hợp con của Lasso dựa trên hình thức ràng buộc và có nhiều cách hiểu bao gồm về mặt hình học , thống kê Bayes và phân tích lồi .
Thống kê Elastic là gì ?
Đây là phương pháp hồi quy trung gian giữa hồi quy ridge và ước lượng lasso
Thực hành ước lượng trên phần mềm R
Cấu hình dữ liệu để ước lượng
Do đặc thù chúng ta sử dụng gói “glmnet” để hồi quy ridge ước lượng lasso hay tính elastic, gói này đòi hỏi dữ liệu đưa vào để xử lý là phải là ma trận, vì vậy chúng ta phải thiết lập ma trận cho dữ liệu trước khi chạy ước lượng bằng gói glmnet này.
setwd("c:/vidu")
library(readxl)
dulieu <-read_excel("tan.xls")
X <- data.matrix(dulieu[c(6,8,9, 10, 11, 14, 16)] )
Y <- data.matrix(dulieu[3] )
Tìm Lambda phù hơp cho dữ liệu
Để phân tích Elastic hay ước lượng ridge chúng ta thường phải hiệu chỉnh bằng hệ số λ , hệ số này phải >=0, vì nếu λ =0 thì mô hình của chúng ta chính là hồi quy bình phương nhỏ nhất ols.
Như vậy bước đầu tiên chúng ta cần tìm là tìm được hệ số hiệu chỉnh lambda cho phù hợp
output<-cv.glmnet(X,Y,lambda=lamb)
bestLamb <-output$lambda.min
Với ước lượng trên ta có λ = 0.5
Tìm hồi quy Ridge
Hồi quy Ridge với Lambda vừa tìm được:
ridge <-glmnet(X,Y,alpha=0,lambda=bestLamb)
Ta được kết quả như sau:
> coef(ridge)
8 x 1 sparse Matrix of class “dgCMatrix”
s0
(Intercept) -3.907128e+01
LnSIZE 9.249388e-01
LnEQAS -2.674133e-01
LOSRES -1.669226e-03
COST -5.471726e-04
CONC 5.331730e+01
CP 3.549367e-04
LNST 1.079888e-03
Phân tích tính Elastic
Với câu lệnh tương tự chúng ta chỉ cần đổi hệ số alpha=0.5
elastic <-glmnet(X,Y,alpha=0.5,lambda=bestLamb)
coef(elastic)
8 x 1 sparse Matrix of class “dgCMatrix”
s0
(Intercept) -2.323027e+01
LnSIZE 6.971197e-01
LnEQAS .
LOSRES .
COST -4.793795e-04
CONC 3.104375e+01
CP 2.370448e-04
LNST 1.165959e-03
Ta thấy kết quả có nhiều thay đổi so với hồi qui ridge rồi . Tiếp theo chúng ta hồi quy Lasso.
Ước lượng Lasso
lasso <-glmnet(X,Y,alpha=1,lambda=bestLamb)
coef(lasso)
Ta thu được kết quả hồi quy lasso như sau:
8 x 1 sparse Matrix of class “dgCMatrix”
s0
(Intercept) -4.5781296955
LnSIZE 0.7474865930
LnEQAS .
LOSRES .
COST -0.0004135294
CONC 3.7467054314
CP .
LNST 0.0013841356
Kết luận sau khi hồi quy
Ta thấy rằng hệ số alpha càng lớn thì làm cho kết quả hồi quy càng chệch đi với hồi quy ols, ta hồi quy ols và ta được kết quả như sau:
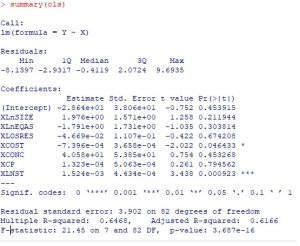
Từ kết quả hồi quy bình phương nhỏ nhất ở trên, chúng ta dễ dàng nhận thấy rằng kết quả thu được từ hồi quy elastic + ước lượng ridge + thống kê lasso, cho chúng ta kết quả rất khác biệt với ols.
Lựa chọn mô hình thống kê phù hợp nhất
Ở đây chúng ta chưa bàn về dùng hồi quy ridge … để khắc phục hiện tượng đa cộng tuyến hay ứng dụng vào việc khác; mà chúng ta chỉ tìm mô hình ước lượng nào phù hợp nhất cho bộ dữ liệu của chúng ta; Để tìm mô hình định lượng ước lượng phù hợp nhất ta dùng 1 trong 2 chỉ tiêu để ước lượng tìm ra mô hình phù hợp là: MSE và R2. Trong ví dụ này tôi dùng R2 để lựa chọn mô hình phù hợp nhất.
Sau khi hồi quy thì chúng ta dễ dàng có được R2 từ công thức sau:
R2= 1 - rss/tss
Ta được:
R2ols = 0.62
R2ridge = 0.64
R2elastic = 0.63
R2lasso = 0.63
Với bộ dữ liệu trên thì kết quả hồi quy Ridge là tốt nhất. Vì có R2 là cao nhất
Ứng dụng
Ngoài 1 cách tiếp cận hồi quy thường được dùng như ols, mle … chúng ta cũng có thể áp dụng hồi quy phi tuyến này, nhằm mục đích tạo ra phương pháp mới mẽ; Ngoài là phương pháp mới chúng ta còn áp dụng phương pháp phi tuyến này để khắc phụ hiện tượng đa cộng tuyến trong mô hình định lượng của mình, đặc biệt là trong mô hình chuỗi thời gian.
Cảm ơn bạn đã đọc tin.








