Hướng dẫn hồi quy tuyến tính OLS: dự báo giá vàng, trong bài hướng dẫn này chúng ta dùng hồi quy ols để dự báo giá vàng, đối với hồi quy bội này ngoài việc tìm nhân tố tác động ra chúng ta còn có thể dự báo một cách dễ dàng. Vẫn như những mô hình định lượng khác mỗi mô hình dự báo điều có những ưu và nhược điểm riêng của nó.
Hồi quy tuyến tính OLS: Dự báo giá vàng
Hồi quy tuyến tính là gì ?
Hồi quy tuyến tính là một phương pháp thống kê được sử dụng để ước tính mối quan hệ tuyến tính giữa hai biến. Nó được sử dụng để dự đoán giá trị của một biến phụ thuộc dựa trên giá trị của một hoặc nhiều biến độc lập.
Hồi quy tuyến tính giả định rằng có một mối quan hệ tuyến tính giữa biến phụ thuộc và các biến độc lập. Để tìm ra mối quan hệ này, phương pháp này sử dụng các dữ liệu quan sát được để tìm ra các hệ số trong phương trình hồi quy tuyến tính. Các hệ số này được sử dụng để xác định mức độ ảnh hưởng của các biến độc lập lên biến phụ thuộc.
Phương trình hồi quy tuyến tính có thể được viết dưới dạng:
y = β0 + β1×1 + β2×2 + … + βnxn + ε
Trong đó:
- y là giá trị của biến phụ thuộc
- x1, x2, …, xn là giá trị của các biến độc lập
- β0, β1, β2, …, βn là các hệ số hồi quy (thường được gọi là “slope”)
- ε là sai số ngẫu nhiên
Phương pháp hồi quy tuyến tính là một công cụ phổ biến trong nhiều lĩnh vực, bao gồm kinh tế học, khoa học xã hội, y học, và các lĩnh vực khác để phân tích dữ liệu và dự đoán các giá trị trong tương lai.
Hồi quy OL là gì ?
OLS (viết tắt của Ordinary Least Squares) là một phương pháp hồi quy tuyến tính để tìm các hệ số của một phương trình tuyến tính, được sử dụng để xác định mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập.

Trong phương pháp OLS, chúng ta tìm kiếm các hệ số của phương trình tuyến tính bằng cách tìm cách tối thiểu hóa sai số giữa giá trị thực tế của biến phụ thuộc và giá trị được dự đoán bằng cách sử dụng các giá trị của biến độc lập. Cụ thể, chúng ta tìm cách tối thiểu hóa tổng bình phương sai số (RSS – Residual Sum of Squares) của các điểm dữ liệu:
RSS = Σ(yi – ŷi)2
Trong đó:
- yi là giá trị thực tế của biến phụ thuộc tại điểm dữ liệu thứ i.
- ŷi là giá trị dự đoán của biến phụ thuộc tại điểm dữ liệu thứ i.
- Σ được sử dụng để tính tổng các sai số của tất cả các điểm dữ liệu.
Phương trình tuyến tính OLS có thể được viết dưới dạng:
y = β0 + β1×1 + β2×2 + … + βnxn + ε
Trong đó:
- y là giá trị của biến phụ thuộc.
- x1, x2, …, xn là giá trị của các biến độc lập.
- β0, β1, β2, …, βn là các hệ số hồi quy (thường được gọi là “slope”).
- ε là sai số ngẫu nhiên.
OLS là một phương pháp phổ biến trong các phân tích thống kê và được sử dụng rộng rãi trong nhiều lĩnh vực, từ kinh tế học đến khoa học xã hội, y học và nhiều lĩnh vực khác.
Ứng dụng hồi quy bội vào dự báo được không ?
Có, hồi quy tuyến tính đa biến là một công cụ mạnh mẽ để dự báo trong nhiều lĩnh vực. Nó cho phép xác định mối quan hệ giữa một biến phụ thuộc và nhiều biến độc lập.
Ứng dụng của hồi quy tuyến tính đa biến là rất đa dạng, ví dụ như:
-
Dự báo giá cổ phiếu hoặc chỉ số tài chính: hồi quy tuyến tính đa biến có thể được sử dụng để dự báo giá cổ phiếu hoặc chỉ số tài chính dựa trên nhiều biến độc lập, chẳng hạn như kết quả kinh doanh, giá dầu, tỷ lệ thất nghiệp, v.v.
-
Dự báo sản lượng: hồi quy tuyến tính đa biến có thể được sử dụng để dự báo sản lượng của một sản phẩm hoặc một dự án dựa trên nhiều yếu tố khác nhau, chẳng hạn như chi phí, thời gian và nguồn lực.
-
Dự báo nhu cầu: hồi quy tuyến tính đa biến có thể được sử dụng để dự báo nhu cầu của một sản phẩm hoặc dịch vụ dựa trên nhiều biến độc lập, chẳng hạn như giá, thu nhập, quảng cáo, v.v.
-
Dự báo hiệu quả của chiến lược kinh doanh: hồi quy tuyến tính đa biến có thể được sử dụng để đánh giá hiệu quả của các chiến lược kinh doanh khác nhau dựa trên nhiều yếu tố khác nhau, chẳng hạn như chi phí quảng cáo, giá cả, v.v.
Tóm lại, hồi quy tuyến tính đa biến là một công cụ quan trọng để dự báo và đánh giá mối quan hệ giữa các biến trong nhiều lĩnh vực.
Các chỉ số đo lượng độ chính xác của dự báo

Các chỉ số đo lường chất lượng dự báo trong hồi quy tuyến tính được sử dụng để đánh giá độ chính xác của mô hình hồi quy tuyến tính. Dưới đây là một số chỉ số phổ biến:
-
R-squared (R2): Đây là một chỉ số phổ biến nhất để đánh giá mức độ phù hợp của mô hình hồi quy tuyến tính. R2 được tính bằng cách chia tổng bình phương sai số giải thích được bởi mô hình cho tổng bình phương sai số ban đầu. R2 có giá trị từ 0 đến 1, và giá trị càng gần 1 thì mô hình càng phù hợp. Tuy nhiên, R2 không phản ánh đầy đủ các khía cạnh của mô hình và có thể bị nhiễu bởi các biến độc lập không liên quan đến biến phụ thuộc.
-
Mean Absolute Error (MAE): Đây là một chỉ số đo lường lỗi dự báo trung bình tuyệt đối giữa giá trị dự đoán và giá trị thực tế. MAE được tính bằng cách lấy trung bình giá trị tuyệt đối của các sai số dự báo. MAE càng thấp thì mô hình càng tốt.
-
Mean Squared Error (MSE): Đây là một chỉ số đo lường lỗi dự báo trung bình bình phương giữa giá trị dự đoán và giá trị thực tế. MSE được tính bằng cách lấy trung bình bình phương của các sai số dự báo. MSE càng thấp thì mô hình càng tốt.
-
Root Mean Squared Error (RMSE): Đây là một chỉ số đo lường lỗi dự báo trung bình bình phương giữa giá trị dự đoán và giá trị thực tế. RMSE được tính bằng cách lấy căn bậc hai của MSE. RMSE càng thấp thì mô hình càng tốt.
-
Mean Absolute Percentage Error (MAPE): Đây là một chỉ số đo lường lỗi dự báo trung bình tuyệt đối dưới dạng phần trăm giữa giá trị dự đoán và giá trị thực tế. MAPE được tính bằng cách lấy trung bình giá trị tuyệt đối của tỷ lệ giữa sai số dự báo và giá trị thực tế, nhân với 100%. MAPE càng thấp thì mô hình càng tốt.
Tóm lại, các chỉ số này giúp đán giá độ chính xác của mô hình hồi quy tuyến tính, tuy nhiên, chúng không phải là tất cả các chỉ số có thể được sử dụng để đánh giá mô hình. Có nhiều chỉ số khác có thể được sử dụng tùy thuộc vào mục đích và bối cảnh sử dụng của mô hình.
Ngoài các chỉ số trên, một số chỉ số khác như tần số sai, độ chính xác, độ phủ, độ tin cậy và giá trị dự đoán có thể được sử dụng để đánh giá độ chính xác của mô hình hồi quy tuyến tính.
Tuy nhiên, việc lựa chọn chỉ số phù hợp để đánh giá mô hình hồi quy tuyến tính còn phụ thuộc vào mục đích sử dụng của mô hình và đặc điểm của dữ liệu được sử dụng. Trong nhiều trường hợp, việc sử dụng nhiều chỉ số đánh giá để đánh giá mô hình là tốt nhất để đảm bảo rằng mô hình được đánh giá một cách toàn diện.
Thực hành dự báo giá vàng trên phần mềm Grelt
Tại sao chọn phần mềm Grelt ?
Grelt (Graphical Environment for Learning and Teaching) là một phần mềm miễn phí mã nguồn mở được sử dụng để giúp sinh viên và giáo viên trong việc thực hiện các phân tích thống kê và dự đoán trong học tập và nghiên cứu.
Dưới đây là một số ưu điểm của phần mềm Grelt:
-
Dễ sử dụng: Grelt có giao diện đồ họa thân thiện, cho phép người dùng dễ dàng thực hiện các phân tích thống kê và dự đoán một cách nhanh chóng và dễ dàng.
-
Đa năng: Grelt hỗ trợ nhiều loại phân tích thống kê và dự đoán, từ phân tích tương quan đến hồi quy tuyến tính, hồi quy logistic và phân tích phân tích hồi quy đa cấp.
-
Hỗ trợ ngôn ngữ R: Grelt được phát triển trên ngôn ngữ lập trình R, cho phép người dùng sử dụng các tính năng mạnh mẽ của R để thực hiện các phân tích thống kê và dự đoán.
-
Miễn phí và mã nguồn mở: Grelt là một phần mềm miễn phí và mã nguồn mở, điều này có nghĩa là bất kỳ ai cũng có thể tải xuống và sử dụng phần mềm một cách tự do, và có thể tham gia vào việc phát triển và cải tiến phần mềm.
-
Phát triển liên tục: Grelt là một dự án phần mềm đang phát triển liên tục, có nghĩa là người dùng có thể mong đợi các cập nhật mới nhất để sử dụng các tính năng mới và cải tiến trong tương lai.
Tóm lại, Grelt là một phần mềm đa năng, dễ sử dụng và miễn phí, được phát triển trên ngôn ngữ lập trình R, và là một công cụ hữu ích cho sinh viên và giáo viên trong việc thực hiện các phân tích thống kê và dự đoán.
Ta hồi quy tuyến tính trên Grelt
Model > Ordinary Least Squares
- Ta đưa biến phụ thuộc vào ô: Dependent Variable
- Đưa nhưng biến độc lập vào ô: Regressor
Bấm OK và có kết quả
| Model 4: OLS, using observations 2018-03-26:2023-01-19 (T = 1259) | ||||
| Dependent variable: CloseLast | ||||
| coefficient | std. error | t-ratio | p-value | |
| const | 1992.898 | 7.598199 | 262.2856 | 0 |
| Date | -0.56655 | 0.010447 | -54.2318 | 0 |
| Mean dependent var | 1635.969 | S.D. dependent var | 246.105 | |
| Sum squared resid | 22814175 | S.E. of regression | 134.7208 | |
| R-squared | 0.700578 | Adjusted R-squared | 0.70034 | |
| F(1, 1257) | 2941.092 | P-value(F) | 0 | |
| Log-likelihood | -7958.58 | Akaike criterion | 15921.16 | |
| Schwarz criterion | 15931.43 | Hannan-Quinn | 15925.02 | |
| rho | 0.992151 | Durbin-Watson | 0.015982 | |
Dự báo
Từ bảng kết quả hồi quy chọn mục: Forecast
Và ta có kết quả:
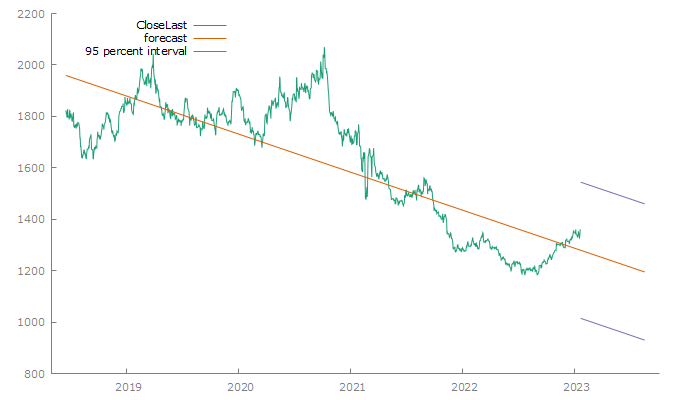
Kết luận Dự báo giá vàng
Đối với mô hình hồi quy tuyến tính OLS chúng ta có thể sử dụng để dự báo dễ dàng rất nhiều, do giá / chỉ số nó rất nhạy với ngoại cảnh các bạn nên dùng những mô hình dự báo khác như: VAR VECM ARIMA HOLTWINER … để dự báo sẽ tốt hơn, còn hồi quy OLS chúng ta nên dự báo chỉ số có độ nhạy thấp hơn, thì sẽ tốt hơn.