hồi quy tuyến tính ols với 10 khuyết tật, ước lượng ols là một trong những hồi quy quan trong mà các bạn thường xuyên sử dụng nhất, vấn đề về hồi quy thì cũng đơn giản, chúng ta có thể thực hiện trên phần mềm excel hay trên các phần mềm thống kê chuyên nghiệp điều có chức năng hồi quy này. Trong bài viết này chúng tôi không tập trung vào hướng dẫn hồi quy hay ước lượng ols mà chỉ tập trung vào các khuyết tật hay sai phạm của hồi quy.
Trong ước lượng hồi quy ols chúng ta thường kiểm tra 5 sai phạm của hồi quy thông dụng, nhưng trên thực tế hay để kết quả hồi quy tăng độ tin cậy, chúng ta còn có thêm 5 kiểm định hay là kiểm tra sai phạm mà chúng ta thường bỏ qua. Trong bài viết này chúng tôi sẽ giới thiệu tất cả 10 khuyết tật của hồi quy và thực hiện trên phần mềm thống kê R. Trong bài viết này mình sẽ chia thành 2 phần: 5 sai phạm cùa quá trình hồi quy ( R2 thấp, biến độc lập không có ý nghĩa thống kê, đa cộng tuyến, phương sai thay đổi, tương quan chuỗi), và 5 khuyết tật của hồi quy. (Ràng buột của hệ số hồi quy, phần dư có phân phối chuẩn, kiểm tra thiếu biến, kiểm tra tính tuyến tính và kiểm tra giá trị ngoại vi).
Mình chia thành 2 phần nhằm mục đích các bạn không mất thời gian đọc hết bài với những kiểm định mà mình đã biết. OK chúng ta bắt đầu bằng việc tạo giả thuyết và kiểm tra dữ liệu.
Nổi dung nổi bậc
I. DỮ LIỆU
1.1 Kết nối dữ liệu
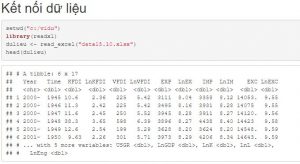
Chúng ta tìm mối tương quan giữa LnGDP với LnIM, để xem giữa nhập khẩu và tăng trưởng kinh tế cố mối quan hệ hay tương quan gì với nhau không ?
1.2 Đồ thị dữ liệu:
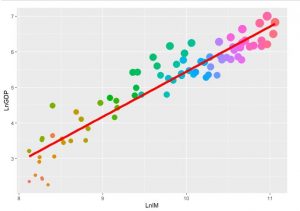
Sau khi chúng ta vẽ đồ thị scatter và abline thì chúng ta dễ dàng nhận thấy rằng, giữa GDP và IM có muốn tương quan tuyến tính cùng chiều. Bởi vậy chúng ta dùng phương pháp hồi quy bình phương nhỏ nhất là chính xác
1.3 Hồi quy OLS
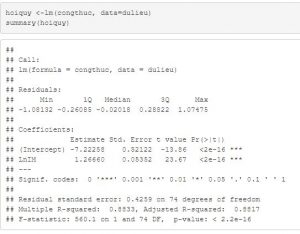
Sau khi hồi quy OLS ta được kết quả như trên, bây giờ để sử dụng được kết quả hồi quy trên chúng ta cần tìm xem trong mô hình chúng ta đưa ra có sai phạm hay không?
II, 5 Sai phạm của mô hình hồi quy OLS
2.1 Biến độc lập có ý nghĩa hay không?
Một trong những vấn đề quan trọng của quá trình hồi quy là biến độc lập có ý nghĩa thống kê hay không? hay nói cách khách là biến độc lập có tác động lên biến phụ thuộc hay không ? Trong ví dụ trên chúng ta tìm mối quan hệ giữa Nhập khẩu có tác động lên Tăng trưởng kinh tế, điều này có nghĩa biến độc lập của chúng ta buột phải có ý nghĩa thống kê. ( Nếu không có ý nghĩa thống kê thì nghiên cứu làm gì ?)
Ta đặt giả thuyết như sau:
- H0: Biến Nhập khẩu không tác động lên tăng trưởng GDP
- H1: Biến Nhập khẩu có tác động đến tăng trưởng GDP
Từ kết quả hồi quy trên, ta có P-value < 0.05, chúng ta bác bỏ H0 chấp nhận H1; Tức biến Nhập khẩu có ảnh hưởng đến tăng trưởng kinh tế.
Nói tóm lại, trong mô hình nghiên cứu biến độc lập phải có ý nghĩa thống kê.
2.2 Mức độ giải thích của mô hình R2
Trong quá trình chạy định lượng co mô hình nghiên cứu, chúng ta thường hay gặp trường hợp là chỉ số R2 quá thấp, điều này biến độc lập giải thích được quá ít biến phụ thuộc.
Trong kết quả hồi quy trên ta có R2 = 0,88; Điều này có nghĩa biến độc lập đã giải thích đến 88% biến phụ thuộc trong mô hình. Đây là một con số tương đối đẹp.
Tới đây chúng ta đặt câu hỏi ? Thế R2 bao nhiêu thì chấp nhận được. Hiện tại chưa có tài liệu nào khẳng định R2 nằm trong khoản nào là tốt. Bởi vậy, chúng tôi chỉ chia sẽ đến các bạn khoản R2 an toàn theo kinh nghiệm bên chúng tôi là 50% < R2 < 90%. Các bạn nên nhớ không nên để R2 > 90% vì rất có thể trong mô hình xuất hiện hiện tượng đa cộng tuyến.
2.3 Đa cộng tuyến
Đa cộng tuyến làm một trọng những sai phạm nghiêm trọng nhất, gần như là không có cách khắc phục, tức là ta không thể nào dùng phương pháp hồi quy tuyến tính OLS này được nữa, phải dùng hồi quy khác, nó sẽ đụng chạm nhiều vấn đề nữa … trong bài viết này chúng tôi không tập trung vào giải quyết vấn đề này.
Chúng ta dùng chỉ số VIF để kiểm tra đa cộng tuyến trong mô hình, nói tới đây thì tại VN chúng ta có 2 trường phái xác nhận đa cộng tuyến là so sánh VIF với 10 và VIF với 5. Trong bài viết này chúng tôi chọn so sánh VIF với 10 cho nó đơn giản và dễ dàng hơn.
Nếu VIF của biến >10 thì ta khẳng định biến nó bị đa cộng tuyến, Nếu dữ liệu đã bị đa cộng tuyến thì bạn nên kiếm dữ liệu khác.
Trong ví dụ của chúng ta do có 1 biến độc lập nên chắc chắn VIF=1, vì vậy không có hiện tượng đa cộng tuyến trong mô hình nghiên cứu.
2.4 Phương sai sai số thay đổi
Lại một trong những giả thuyết quan trọng của hồi quy tuyến tính nữa là, phương sai của sai số phải không thay đổi, bởi vậy chúng ta cần kiểm tra giả thuyết này sau khi hồi quy, để kiểm tra chúng ta có thể dùng đồ thị hay dùng kiểm định điều được, trước tiên ta xem đồ thị của phuong sai như thế nào?
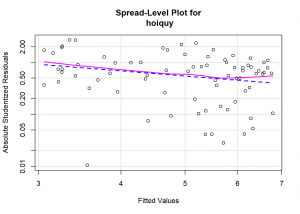
Ta thấy đường phương sai( màu hồng) gần như trùng với đường màu xanh, nhưng lại có xu hướng tách ra và có chiều hướng giảm dần , chúng ta có thể khẳng định rằng phương sai sai số thay đổi, Để nhìn đồ thị đồ hỏi phải trực quan và kinh nghiệm, nếu các bạn không quen có thể dùng kiểm định cho nó đơn giản
Ta dùng kiểm định Breusch-Pagan test, có kết quả như sau:
## studentized Breusch-Pagan test
##
## data: hoiquy
## BP = 7.4486, df = 1, p-value = 0.006349
Ta đặt giả thuyết như sau:
- H0: Phương sai sai số cố định
- H1: Phương sai sai số thay đổi
Từ kết quả trên, ta có P-value < 0.05, nên ta bác bỏ H0 chấp nhận H1 nên mô hình nghiên cứu có hiện tượng phương sai số thay đổi.
2.5 Tự tương quan
Trong mô hình nghiên cứu chúng ta cần phải kiểm tra thêm hiện tượng tự tương quan, để kiểm tra hiện tượng tương quan chuỗi chúng ta sử dụng kiểm định Durbin – Watson test
##
## Durbin-Watson test
##
## data: hoiquy
## DW = 0.87624, p-value = 1.738e-08
## alternative hypothesis: true autocorrelation is greater than 0
Ta có P-value < 0.05, nên mô hình nghiên cứu có hiện tượng tự tương quan chuỗi.
Trên đây là ta đã kiểm định xong 5 sai phạm của mô hình hồi quy , sau đây chúng ta sẽ kiểm tra 5 khuyết tật của mô hình hồi quy ( Như đã nói ở đây, khuyết tật và sai phạm là giống nhau, chúng tôi dùng như thế để cho các bạn dễ phân lớp ra)
III, 5 Khuyết tật của hồi quy tuyến tính
3.1 Ràng buột hệ số hồi quy
Kiểm định sự Ràng buột của hệ số hồi quy hay còn gọi là các hệ số hồi quy không đồng thời bằng 0, đây là một kiểm định các bạn thật sự khó hiểu về ý nghĩa của nó, diễn giải nôm na là các biến độc lập trong mô hình có ít nhất là 1 biến độc lập có tác động đến biến phụ thuộc, để biết được vấn đề này chúng ta sử dụng kiểm định Wald
## Linear hypothesis test
##
## Hypothesis:
## LnIM = 1.2667
##
## Model 1: restricted model
## Model 2: LnGDP ~ LnIM
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 75 13.425
## 2 74 13.425 1 5.9352e-07 0 0.9986
Ta có P-value > 0.05 nên ta khẳng định rằng có ít nhất 1 biến độc lập tác động lên biến phục thuộc hay là các biến độc lập không đồng thời bằng 0.
3.2 Kiểm tra bỏ xót biến
Để kiểm tra thiếu biến trong mô hình nghiên cứu chúng ta sử dùng kiểm định RAMSEY’S RESET TEST
##
## RESET test
##
## data: hoiquy
## RESET = 15.234, df1 = 1, df2 = 73, p-value = 0.0002096
- H0: Mô hình nghiên cứu không bị bỏ xót biến
- H1: Mô hình nghiên cứu bỏ xót biến
Ta có P-value < 0.05, bởi vậy mô hình nghiên cứu của chúng ta đã bỏ xót biến.
Vấn đề đặt ra ở đây là mô hình bỏ xót biến, vậy biến bỏ xót là biến nào ?
3.3 Phần dư có phân phối chuẩn
Một trong những kiểm định mà chúng ta thường hay bỏ qua đó là kiểm tra phân phối chuẩn cho phần dư, đặc biệt là rất cần thiết cho những mô hình nghiên cứu có quan sát ít. Để kiểm tra phân phối chuẩn chúng ta có thể dùng đồ thị histogram để xem xét
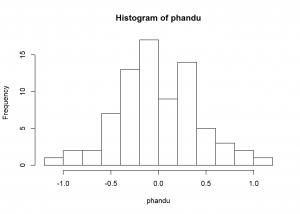
Từ đồ thị histogram chúng ta dễ dàng nhận thấy rằng phần dư đã có phân phối chuẩn, vì phần dư có hình CHUÔNG ( tuy là không đẹp lắm: tương đối cân đối nhưng không nhọn). Nếu vấn đề về đồ thị làm chúng ta bối rối chúng ta sẽ sử dụng kiểm định để xác nhận phân phối có chuẩn không?
##
## Title:
## Jarque - Bera Normalality Test
##
## Test Results:
## STATISTIC:
## X-squared: 0.6092
## P VALUE:
## Asymptotic p Value: 0.7374
##
## Description:
## Thu Mar 26 12:00:45 2020 by user: Admin
Từ kiểm định Jarque – Bera, chúng ta có P-value > 0.05, chúng ta suy ra là phân phối của phần dư là chuẩn. Nên chưa an tâm chúng ta tiếp tục kiểm tra
##
## Title:
## Shapiro - Wilk Normality Test
##
## Test Results:
## STATISTIC:
## W: 0.9892
## P VALUE:
## 0.7726
##
## Description:
## Thu Mar 26 12:00:45 2020 by user: Admin
Kết quả của kiểm định Shapiro – Wilk tương tự
Chúng ta có thể kết luận phần dư đã phân phối chuẩn.
3.4 Mô hình nghiên cứu là tuyến tính
Cái kiểm định này thì ít người sử dụng, nhưng chúng tôi vấn giới thiệu đến các bạn tham khảo. Để xác nhận kết quả của kiểm định chúng ta sử dụng đồ thị như sau:
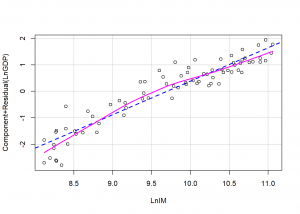
Ta đồ thị chúng ta dễ dàng nhận thấy rằng, phần nước lượng và phần dư bám sát vào nhau và có hình dạng là tuyến tính.
3.5 Kiểm tra quan sát ngoại vi
Tức là trong kiểm định này, chúng ta có loại các quan sát bất thường hay còn gọi là ngoại vi hay không ? ( Hay chúng ta thường hay dùng thuật ngữ lại loại bỏ outlier
## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
## rstudent unadjusted p-value Bonferroni p
## 6 -2.701985 0.0085658 0.651
Từ kiểm định trên chúng ta có dòng thứ 6 có outlier
Trên đây là chúng tôi đã hướng dẫn các bạn 10 kiểm định quan trọng để giúp cho mô hình hồi quy tuyến tính có độ tin cậy cao./.