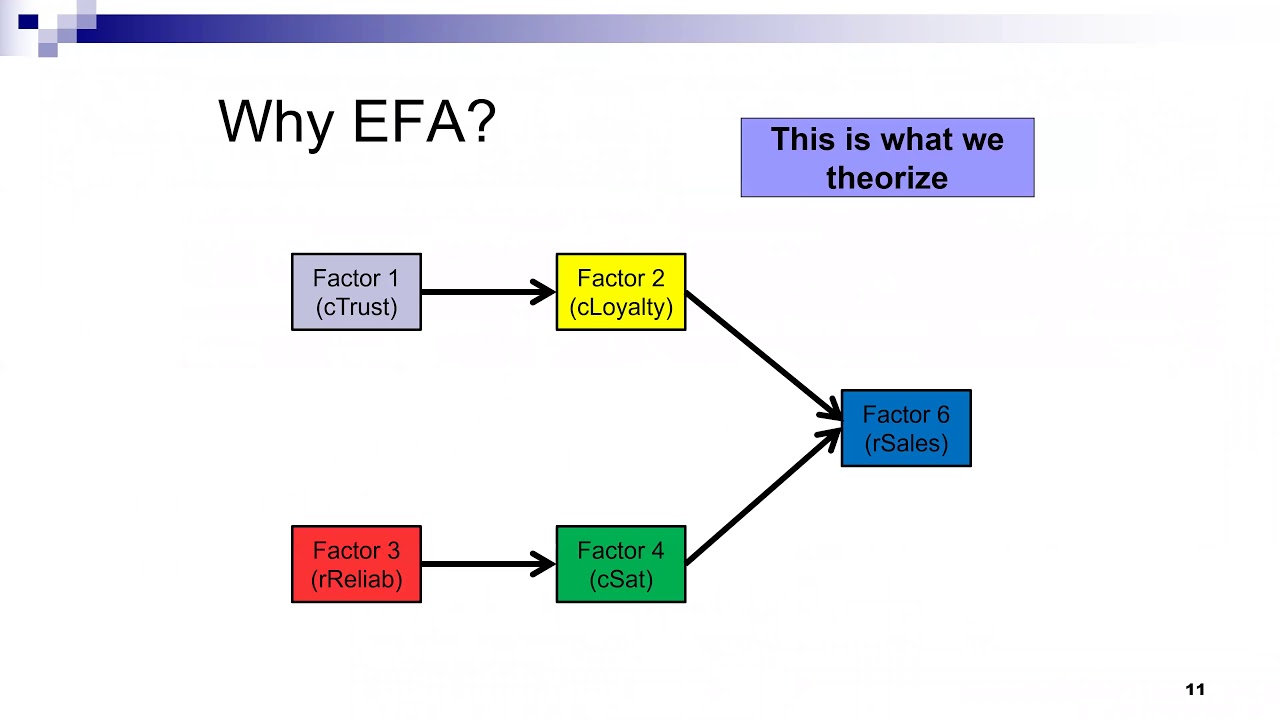
Hồi quy phân cấp (Hierarchical regression) không phải là hồi quy tuyến tính phân cấp (Hierarchical linear regression). Hồi quy phân cấp là phương pháp hồi quy so sách phân cấp các mô hình hồi quy lồng ghép vào nhau. Trong ví dụ này chúng tôi sẽ thực hiện thực hành trên phần mềm thống kê R. Để thực hiện hồi quy phân cấp thì chúng ta có thể thực hiện dễ dàng trên SPSS, Stata, R.
Nổi dung nổi bậc
Khi nào sử dụng hồi quy phân cấp ?
Hồi quy phân cấp là một cách để hiển thị nếu các biến quan tâm của bạn giải thích một lượng phương sai có ý nghĩa thống kê trong Biến phụ thuộc (DV) của bạn sau khi tính tất cả các biến khác. Đây là một khuôn khổ để so sánh mô hình chứ không phải là một phương pháp thống kê. Trong khung này, bạn xây dựng một số mô hình hồi quy bằng cách thêm các biến vào mô hình trước đó ở mỗi bước; các mô hình sau luôn bao gồm các mô hình nhỏ hơn trong các bước trước. Trong nhiều trường hợp, mối quan tâm của chúng tôi là xác định xem các biến mới được thêm vào có cho thấy sự cải thiện đáng kể trong R không2R2 (tỷ lệ phương sai được giải thích trong DV theo mô hình).
Điểm mạnh của hồi quy phân cấp
Có một số cách khác để phân tích dữ liệu phân cấp, mặc dù hầu hết trong số chúng có một số vấn đề. Đầu tiên, các kỹ thuật thống kê truyền thống có thể được sử dụng. Người ta có thể phân tách các biến thứ tự cao hơn cho cấp độ cá nhân và do đó tiến hành phân tích ở cấp độ cá nhân này (ví dụ: gán các biến lớp cho cấp độ cá nhân). Vấn đề với phương pháp này là nó sẽ vi phạm giả định độc lập, và do đó có thể làm sai lệch kết quả của chúng tôi. Điều này được gọi là sai lầm nguyên tử. Một cách khác để phân tích dữ liệu bằng các phương pháp thống kê truyền thống là tổng hợp các biến cấp độ riêng lẻ thành các biến bậc cao hơn và sau đó tiến hành phân tích ở cấp độ cao hơn này. Vấn đề với cách tiếp cận này là nó loại bỏ tất cả thông tin trong nhóm (bởi vì nó lấy trung bình của các biến cấp độ riêng lẻ). Có đến 80 809090 phương sai có thể bị lãng phí và mối quan hệ giữa các biến tổng hợp bị thổi phồng và do đó bị biến dạng. Điều này được gọi là sai lầm sinh thái , và theo thống kê, loại phân tích này dẫn đến giảm sức mạnh bên cạnh việc mất thông tin.
Một cách khác để phân tích dữ liệu phân cấp sẽ thông qua mô hình hệ số ngẫu nhiên. Mô hình này giả định rằng mỗi nhóm có một mô hình hồi quy khác nhau, có độ chặn và độ dốc riêng. Bởi vì các nhóm được lấy mẫu, mô hình giả định rằng các phần chặn và độ dốc cũng được lấy mẫu ngẫu nhiên từ một quần thể các nhóm chặn và độ dốc. Điều này cho phép phân tích trong đó người ta có thể giả định rằng độ dốc là cố định nhưng việc chặn được phép thay đổi. Tuy nhiên, điều này trình bày một vấn đề, vì các thành phần riêng lẻ là độc lập nhưng các thành phần nhóm độc lập giữa các nhóm, nhưng phụ thuộc trong các nhóm. Điều này cũng cho phép phân tích trong đó các sườn là ngẫu nhiên; tuy nhiên, mối tương quan của các thuật ngữ lỗi (nhiễu) phụ thuộc vào giá trị của các biến cấp độ cá nhân. Do đó, vấn đề với việc sử dụng mô hình hệ số ngẫu nhiên để phân tích dữ liệu phân cấp là vẫn không thể kết hợp các biến thứ tự cao hơn.
Các bước thực hiện hồi qui phân cấp
- Xây dựng các mô hình hồi quy lồng ghép vào nhau
- Chạy ANOVA để tính R2 và hệ số hồi quy
-
So sánh tổng Phương sai qua các mô hình
- Tính toán tổng Phương sai khác biệt
- Tìm thống kê F và P-value của Phương sai khác biệt
- Tính R2 tăng lên khi có Phương sai khác biệt
Thực hiện hồi quy phân cấp trên R
Ta xây dựng mô hình lồng ghép như sau
m1 <- lm(GIADV~NGANG+DAI, data=dulieu)
m2 <- lm(GIADV~NGANG + DAI + DTICH + KCACH, data=dulieu)
m3 <- lm(GIADV~NGANG + DAI + DTICH + KCACH + MTIEN + STHUONG, data=dulieu)
m4 <- lm(GIADV~NGANG + DAI + DTICH + KCACH + MTIEN + STHUONG +SLAU +PHONG, data=dulieu)
Ta được kết quả hồi quy của 4 mô hình như sau:
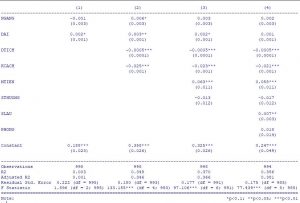
Phân tích ANOVA
## Analysis of Variance Table
##
## Model 1: GIADV ~ NGANG + DAI
## Model 2: GIADV ~ NGANG + DAI + DTICH + KCACH
## Model 3: GIADV ~ NGANG + DAI + DTICH + KCACH + MTIEN + STHUONG
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 995 49.094
## 2 993 32.057 2 17.0371 272.176 < 2.2e-16 ***
## 3 991 31.016 2 1.0408 16.627 7.897e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Từ kết quả phân tích ANOVA trên ta được, ta dễ dàng chọn được mô hình 3 là tối ưu.
Kết luận:
Mô hình phân tích hồi quy phân cấp được dùng hay ứng dụng rộng rãi trong chính sách kinh tế, kinh tế xã hội …