bất bình đằng thu nhập, cách tính hệ số GINI trong phần mềm Excel, Stata, R … ý nghĩa của hệ số GINI, công thức xây dựng tính bất bình đẳng thu nhập, ứng dụng phân tích bất bình đẳng trong các phần mềm thống kê chuyên nghiệp …
-
Nổi dung nổi bậc
Bất bình đẳng thu nhập là gì ?
Trong kinh tế học , các hệ số Gini , đôi khi được gọi là chỉ số Gini hoặc tỷ lệ Gini , là một thước đo của sự phân tán thống kê nhằm đại diện cho thu nhập hay phân phối sự giàu có của người dân của một quốc gia, và là phép đo bất bình đẳng được sử dụng phổ biến nhất . Nó được phát triển bởi nhà thống kê và nhà xã hội học người Ý Corrado Gini và được xuất bản trong bài báo năm 1912 của ông Biến đổi và biến đổi (Tiếng Ý : Variabilità e mutabilità ).
Hệ số Gini đo lường sự bất bình đẳng giữa các giá trị của phân phối tần số (ví dụ: mức thu nhập ). Hệ số Gini bằng 0 biểu thị sự bình đẳng hoàn hảo, trong đó tất cả các giá trị đều giống nhau (ví dụ: mọi người đều có cùng thu nhập). Hệ số Gini của một (hoặc 100%) biểu thị sự bất bình đẳng tối đa giữa các giá trị (ví dụ: đối với một số lượng lớn người, trong đó chỉ có một người có tất cả thu nhập hoặc tiêu dùng và tất cả những người khác không có, hệ số Gini sẽ gần như một ). Đối với các nhóm lớn hơn, các giá trị gần với một là rất khó xảy ra trong thực tế. Với sự bình thường hóa của cả dân số tích lũy và phần thu nhập tích lũy được sử dụng để tính hệ số Gini, biện pháp này không quá nhạy cảm với các đặc thù của phân phối thu nhập, mà chỉ dựa vào cách thu nhập thay đổi so với các thành viên khác trong dân số . Ngoại lệ cho điều này là trong phân phối lại thu nhập dẫn đến thu nhập tối thiểu cho tất cả mọi người. Khi dân số được sắp xếp, nếu phân phối thu nhập của họ xấp xỉ một hàm nổi tiếng, thì một số giá trị đại diện có thể được tính toán.
Hệ số Gini đã được đề xuất bởi Gini như một biện pháp của bất bình đẳng của thu nhập hay sự giàu có . Đối với các nước OECD , vào cuối thế kỷ 20, xem xét ảnh hưởng của thuế và thanh toán chuyển khoản , hệ số Gini thu nhập dao động trong khoảng 0,24 đến 0,49, trong đó, thấp nhất là Mexico và Mexico là cao nhất. Các quốc gia châu Phi có hệ số Gini trước thuế cao nhất trong năm 20082002009, với Nam Phi cao nhất thế giới, ước tính khác nhau là 0,63 đến 0,7, mặc dù con số này giảm xuống 0,52 sau khi trợ giúp xã hội được thực hiện vào tài khoản, và giảm xuống còn 0,47 sau khi đánh thuế. Hệ số Gini thu nhập toàn cầu năm 2005 được ước tính là từ 0,61 đến 0,68 bởi nhiều nguồn khác nhau.
Có một số vấn đề trong việc diễn giải một hệ số Gini. Giá trị tương tự có thể là kết quả của nhiều đường cong phân phối khác nhau. Cấu trúc nhân khẩu học cần được tính đến. Các quốc gia có dân số già, hoặc bùng nổ trẻ em, trải qua hệ số Gini trước thuế ngày càng tăng ngay cả khi phân phối thu nhập thực tế cho người lớn đang làm việc không đổi. Các học giả đã nghĩ ra hơn một chục biến thể của hệ số Gini.
2. Hệ số GINI
Hệ số Gini là một số duy nhất nhằm đo lường mức độ bất bình đẳng trong phân phối. Nó thường được sử dụng trong kinh tế học để đo lường mức độ giàu có hoặc phân phối thu nhập của một quốc gia lệch khỏi phân phối hoàn toàn bình đẳng.
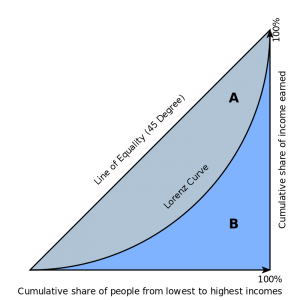
Hệ số Gini thường được xác định một cách toán học dựa trên đường cong Lorenz , biểu đồ tỷ lệ của tổng thu nhập của dân số (trục y) được tích lũy theo x dưới cùng của dân số (xem sơ đồ). Đường ở 45 độ như vậy đại diện cho sự bình đẳng hoàn hảo của thu nhập. Hệ số Gini sau đó có thể được coi là tỷ lệ của khu vực nằm giữa đường đẳng thức và đường cong Lorenz (được đánh dấu A trong sơ đồ) trên tổng diện tích dưới đường đẳng thức (được đánh dấu A và B trong sơ đồ) ; tức là G = A / ( A + B ) . Nó cũng bằng 2A và đến 1 – 2 B do thực tế là A + B = 0,5 (vì tỷ lệ trục từ 0 đến 1).
Nếu tất cả mọi người có thu nhập không âm (hoặc giàu có, tùy theo từng trường hợp), hệ số Gini về mặt lý thuyết có thể dao động từ 0 (hoàn toàn bình đẳng) đến 1 (bất bình đẳng hoàn toàn); đôi khi nó được biểu thị dưới dạng phần trăm nằm trong khoảng từ 0 đến 100. Trong thực tế, cả hai giá trị cực trị đều không đạt được. Nếu các giá trị âm là có thể (chẳng hạn như sự giàu có âm của những người có nợ), thì về mặt lý thuyết, hệ số Gini có thể lớn hơn 1. Thông thường trung bình (hoặc tổng) được giả định là dương, quy định hệ số Gini nhỏ hơn 0.
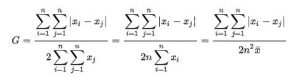
Một cách tiếp cận khác là xác định hệ số Gini bằng một nửa chênh lệch tuyệt đối trung bình tương đối , tương đương về mặt toán học với định nghĩa đường cong Lorenz. Sự khác biệt tuyệt đối trung bình là chênh lệch tuyệt đối trung bình của tất cả các cặp vật phẩm của dân số và chênh lệch tuyệt đối trung bình tương đối là chênh lệch tuyệt đối trung bình chia cho trung bình , để bình thường hóa cho quy mô. Nếu x i là của cải hoặc thu nhập của người i và có n người, thì hệ số Gini G được cho bởi:
Ứng dụng tính Hệ số bất bình đẳng thu nhập
3. Tính hệ số GINI trên Excel
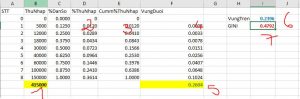
Các bạn thực hiện từng bước như trong hình vẽ, theo công thức giải thích bên dưới:
1: B11= =SUM(B2:B10)
2: D3 = =B3/$B$11
3. E3=D3+E2
4. F3=(E3+E2)/2*0.125
5. F11 =SUM(F3:F10)
6. I2 = 0.5-F11
7. I2 =I2/0.5 = 0.4792 => Đây là hệ số GINI
Nói chung để tính hệ số GINI trên excel thì tương đối phức tạp, yêu cầu chúng ta phải hiểu nhiều về đường cong thu nhập Lorenz, bởi vậy trên Stata hay R … luôn luôn có những hàm tính Hệ số bất bình đẳng nhanh chóng và tiện ích.
4. Tính hệ số GINI trên Stata
Để thực hiện tính hệ số bất bình đằng thu nhập của GINI trên stata ta thực hiện 2 bước đơn giản như sau:
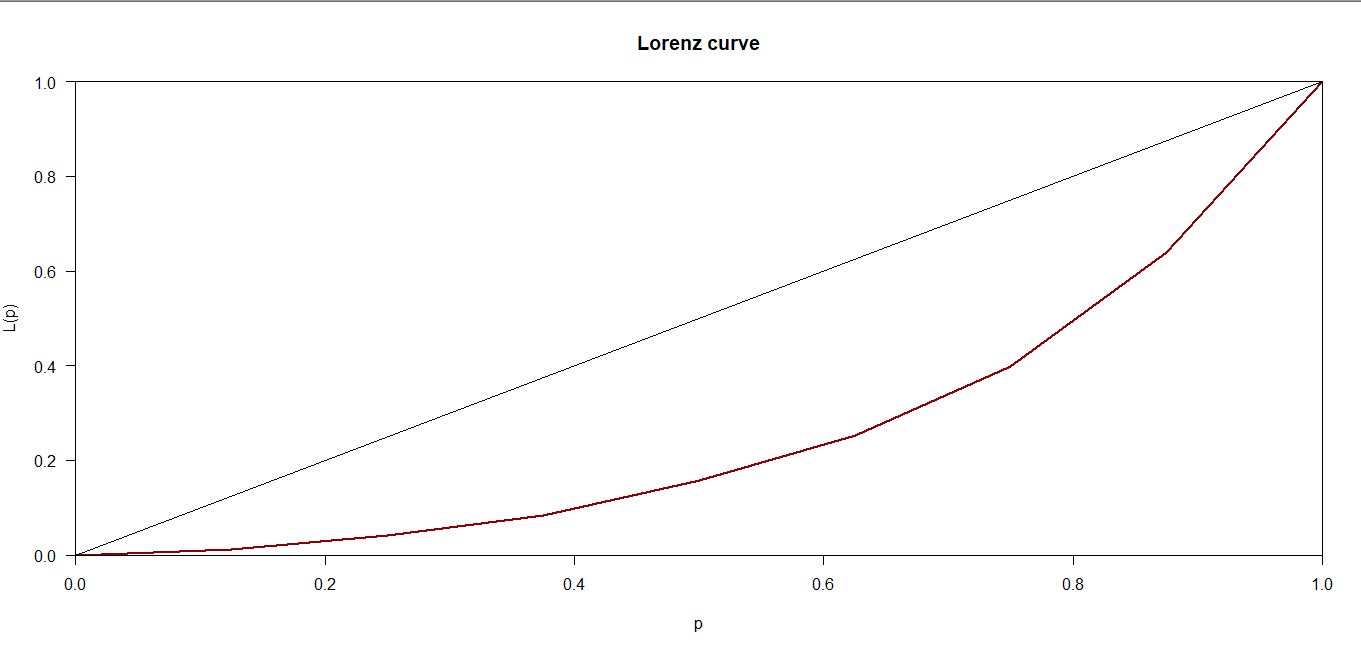
Bước 1: Vẽ đồ thị Lorenz
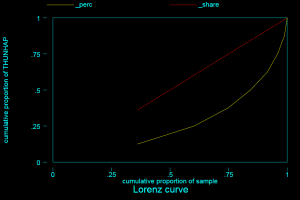
Nhìn vào đồ thị thì chúng ta sẽ dễ dàng nhận thấy rằng 2 phần A và B là tương đương nhau, có thể khẳng định hệ số GINI trong khoảng ( 0.4 – 0.6), nhưng chúng ta cần một số cụ thể như cách tính của Excel.
Bước 2: Tính GINI
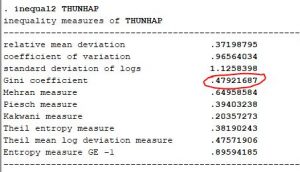
Ta có hệ số bất bình đẳng thu nhập cũng là 0.4792
Ta thấy rõ ràng, là cách tính trên Stata nó rất đơn giản và hiệu quả.
Ngoài phần mềm Stata ra, thì cũng có thể tính GINI trên phần mềm rất thông dụng là R
5. Tính hệ số GINI trên R
library(reldist)
gini(THUNHAP) = 0.4792169
Chúng ta cũng có kết quả là GINI= 0.4792169
6. Tóm lại:
Để tính hệ số GINI thì chúng ta nên dùng phần mềm Stata hay R để cho việc tính toán trở nên dễ dàng hơn