danh sách mô hình định lượng thông dụng, được thongke.club lên danh sách cho các bạn có cái nhìn thông dụng trong quá trình nghiên cứu khoa học hay hoàn thành bài luận riêng của mình. Trong quá trình nghiên cứu khoa học thì không có mô hình kinh tế lượng nào tốt nhất hay có một mô hình nào dở hết; quan trọng là khi sử dụng mô hình kinh tế lượng vào thực tiễn chúng ta ” khai thác” được cái ” cốt lõi” của mô hình.
Khi lên danh sách này chúng tôi có kèm theo cái ứng dụng của mô hình khuyến nghị, nhưng đây chỉ là khuyến nghị khi áp dụng tùy từng ứng dụng thực tế khác nhau mà cách dùng khác nhau, sau đây là danh sách các mô hình định lượng thông dụng chúng ta cần xem xét:
DỮ LIỆU 1 CHIỀU
Hồi quy OLS
Trong thống kê , bình phương tối thiểu thông thường ( OLS ) là một loại phương pháp bình phương tối thiểu tuyến tính để ước tính các tham số chưa biết trong mô hình hồi quy tuyến tính . OLS chọn các tham số của hàm tuyến tính của một tập hợp các biến giải thích theo nguyên tắc bình phương tối thiểu: tối thiểu hóa tổng bình phương của sự khác biệt giữa biến phụ thuộc được quan sát (giá trị của biến được dự đoán) trong tập dữ liệu đã cho và các biến được dự đoán bởi hàm tuyến tính.
Ứng dụng cực kỳ nhiều trong nhiều lĩnh vực như: kinh tế, thống kê, y tế, kỹ thuật …
Hồi quy logit
Trong thống kê , mô hình logistic (hoặc mô hình logit ) được sử dụng để mô hình xác suất của một lớp hoặc sự kiện nào đó tồn tại như vượt qua / thất bại, thắng / thua, sống / chết hoặc khỏe / ốm. Điều này có thể được mở rộng để mô hình hóa một số loại sự kiện như xác định xem một hình ảnh có chứa mèo, chó, sư tử, v.v … Mỗi đối tượng được phát hiện trong hình ảnh sẽ được gán một xác suất từ 0 đến 1 và tổng cộng vào một .
Hồi quy tobit
Các mô hình Tobit đề cập đến một lớp học của mô hình hồi quy trong đó phạm vi quan sát của biến phụ thuộc được kiểm duyệt một cách nào đó. Thuật ngữ này được đặt ra bởi Arthur Goldberger trong tham chiếu đến James Tobin, người đã phát triển các mô hình năm 1958 để giảm thiểu các vấn đề của zero-thổi phồng dữ liệu cho các quan sát chi tiêu hộ gia đình đối với hàng hóa lâu bền. Bởi vì phương pháp của Tobin có thể dễ dàng được mở rộng để xử lý các mẫu bị cắt ngắn và các mẫu không được chọn ngẫu nhiên khác, một số tác giả áp dụng định nghĩa rộng hơn về mô hình Tobit bao gồm các trường hợp này.
Hồi quy probit
Trong thống kê , mô hình probit là một loại hồi quy trong đó biến phụ thuộc chỉ có thể lấy hai giá trị, ví dụ kết hôn hoặc không kết hôn. Từ này là một portmanteau , xuất phát từ khả năng thăm dò + un it . Mục đích của mô hình là ước tính xác suất quan sát với các đặc điểm cụ thể sẽ rơi vào một trong các loại cụ thể; hơn nữa, phân loại các quan sát dựa trên xác suất dự đoán của chúng là một loại mô hình phân loại nhị phân .
Hồi quy 2sls
Trong thống kê , kinh tế lượng , dịch tễ học và các ngành liên quan, phương pháp biến công cụ ( IV ) được sử dụng để ước tính mối quan hệ nhân quả khi các thí nghiệm được kiểm soát là không khả thi hoặc khi điều trị không được chuyển giao thành công cho mọi đơn vị trong một thí nghiệm ngẫu nhiên. Theo trực giác, IV được sử dụng khi một biến quan tâm giải thích có tương quan với thuật ngữ lỗi, trong trường hợp bình phương nhỏ nhất bình thường và ANOVA cho sai lệchcác kết quả. Một công cụ hợp lệ gây ra những thay đổi trong biến giải thích nhưng không có tác động độc lập đến biến phụ thuộc, cho phép nhà nghiên cứu khám phá tác động nhân quả của biến giải thích lên biến phụ thuộc.
Hồi quy 3sls
3SLS cũng giống như 2SLS để hồi quy biến công cụ, khắc phục hiện tượng nội sinh trong mô hình.
3SLS có được ước tính bình phương tối thiểu ba giai đoạn của một tập hợp các phương trình phi tuyến. Đây là trường hợp đặc biệt của LSQ với các tùy chọn được đặt cho ước tính 3SLS. Mục LSQ có một mô tả đầy đủ hơn về lệnh.
Hồi quy heckman
Các chỉnh Heckman là kỹ thuật thống kê để điều chỉnh sai lệch từ mẫu được lựa chọn không phải là ngẫu nhiên hay tình cờ biến phụ thuộc cắt ngắn , một vấn đề phổ biến trong định lượng khoa học xã hội khi sử dụng dữ liệu quan sát . Về mặt khái niệm, điều này đạt được bằng cách mô hình hóa rõ ràng xác suất lấy mẫu riêng lẻ của từng quan sát (cái gọi là phương trình lựa chọn) cùng với kỳ vọng có điều kiện của biến phụ thuộc (phương trình kết quả được gọi là). Hàm khả năng kết quả tương tự về mặt toán học với mô hình Tobitđối với các biến phụ thuộc bị kiểm duyệt , một kết nối được James Heckman rút ra lần đầu tiên vào năm 1976. Heckman cũng đã phát triển một cách tiếp cận hàm điều khiển hai bước để ước tính mô hình này, làm giảm gánh nặng tính toán khi phải ước tính cả hai phương trình cùng nhau, mặc dù với chi phí không hiệu quả . Heckman nhận giải thưởng tưởng niệm Nobel về khoa học kinh tế năm 2000 cho công trình của mình trong lĩnh vực này.
Hồi quy GMM
Trong kinh tế lượng và thống kê , phương pháp tổng quát của các khoảnh khắc ( GMM ) là một phương pháp chung để ước tính các tham số trong các mô hình thống kê . Thông thường, nó được áp dụng trong ngữ cảnh của các mô hình bán tổng thể , trong đó tham số quan tâm là hữu hạn, trong khi hình dạng đầy đủ của hàm phân phối dữ liệu có thể không được biết và do đó ước tính khả năng tối đa không được áp dụng.
Hồi quy LCA
Phân tích lớp tiềm ẩn (LCA) là một kỹ thuật đa biến có thể được áp dụng cho các mục đích cụm, yếu tố hoặc hồi quy.
Phân tích lớp tiềm ẩn (LCA) thường được sử dụng bởi nhà nghiên cứu trong các trường hợp bắt buộc phải thực hiện phân loại các trường hợp thành một tập hợp các lớp tiềm ẩn. Nó được thực hiện trên các lớp tiềm ẩn và dựa trên các loại biến chỉ báo phân loại. Trong LCA, các biến chỉ báo là các biến được gán là ‘1’ nếu điều kiện của chúng là đúng và được gán khác là ‘0.’
Hồi quy Mutilnomial logit
Trong thống kê , hồi quy logistic đa thức là một phương pháp phân loại tổng quát hóa hồi quy logistic cho các vấn đề đa giác , tức là có nhiều hơn hai kết quả riêng biệt có thể xảy ra. [1] Đó là một mô hình được sử dụng để dự đoán xác suất của các kết quả khác nhau có thể có của một biến phụ thuộc phân loại , được đưa ra một tập hợp các biến độc lập (có thể có giá trị thực, có giá trị nhị phân, có giá trị phân loại , v.v.)
….
DỮ LIỆU DATA PANEL
Khi mô hình dữ liệu có mô hình gì thì trong data panel cũng có mô hình đó, sau đây chúng tôi liệt kê ra những mô hình cực kỳ thông dụng trong mô hình định lượng, dưới đây là danh sách mô hình định lượng thông dụng nhất:
Hồi quy bảng (OLS + REM + FEM)
Hồi quy bảng (MG + PMG + DFE)
Hồi quy PVAR
Hồi quy GMM
Hồi quy logit bảng
…..
DỮ LIỆU THỜI GIAN

Hồi quy VAR
Vector autorewardsion ( VAR ) là một mô hình quy trình ngẫu nhiên được sử dụng để nắm bắt các phụ thuộc tuyến tính giữa các chuỗi thời gian . Các mô hình VAR tổng quát hóa mô hình tự phát đơn biến (mô hình AR) bằng cách cho phép nhiều hơn một biến phát triển. Tất cả các biến trong VAR nhập mô hình theo cùng một cách: mỗi biến có một phương trình giải thích sự tiến hóa của nó dựa trên các giá trị bị trễ của chính nó , các giá trị bị trễ của các biến mô hình khác và một thuật ngữ lỗi . Mô hình hóa VAR không đòi hỏi nhiều kiến thức về các lực ảnh hưởng đến một biến như các mô hình cấu trúc với các phương trình đồng thời: Kiến thức duy nhất cần có là một danh sách các biến có thể được đưa ra giả thuyết để ảnh hưởng lẫn nhau.
Mô hình VECM
Cách tiếp cận Engle của Granger như mô tả ở trên bị một số điểm yếu. Cụ thể, nó chỉ bị giới hạn ở một phương trình duy nhất với một biến được chỉ định là biến phụ thuộc, được giải thích bởi một biến khác được coi là yếu kém ngoại lệ đối với các tham số quan tâm. Nó cũng dựa vào việc giả định chuỗi thời gian để tìm hiểu xem các biến là I (0) hay I (1). Những điểm yếu này có thể được giải quyết thông qua việc sử dụng thủ tục của Johansen. Ưu điểm của nó bao gồm việc giả vờ là không cần thiết, có thể có nhiều mối quan hệ hợp nhất, tất cả các biến được coi là nội sinh và các xét nghiệm liên quan đến các tham số dài hạn là có thể. Mô hình kết quả được gọi là mô hình sửa lỗi vectơ (VECM), vì nó thêm các tính năng sửa lỗi cho mô hình đa yếu tố được gọi là tự động vectơ(VAR). Thủ tục được thực hiện như sau:
- Bước 1: ước tính VAR không giới hạn liên quan đến các biến không cố định
- Bước 2: Kiểm tra sự hợp nhất bằng cách sử dụng kiểm tra Johansen
- Bước 3: Hình thành và phân tích VECM.
Mô hình ARDL
Mô hình tự phân phối hồi quy tự động (ARDL) đóng vai trò quan trọng khi cần phân tích kịch bản kinh tế. Trong một nền kinh tế, sự thay đổi trong bất kỳ biến số kinh tế nào có thể mang lại sự thay đổi trong một biến số kinh tế khác ngoài thời gian.Sự thay đổi này trong một biến không phải là những gì phản ánh ngay lập tức, nhưng nó phân phối trong các giai đoạn tương lai. Không chỉ các biến kinh tế vĩ mô, các biến khác như thua lỗ hoặc lợi nhuận mà một công ty kiếm được trong một năm có thể ảnh hưởng đến hình ảnh thương hiệu của một tổ chức trong giai đoạn này.
Mô hình ECM
Một mô hình sửa lỗi (ECM) thuộc về một loại mô hình chuỗi nhiều thời gian được sử dụng phổ biến nhất cho dữ liệu trong đó các biến cơ bản có xu hướng ngẫu nhiên dài hạn, còn được gọi là hợp nhất . ECM là một cách tiếp cận dựa trên lý thuyết hữu ích để ước tính cả tác động ngắn hạn và dài hạn của chuỗi thời gian này đến chuỗi thời gian khác. Thuật ngữ sửa lỗi liên quan đến thực tế là độ lệch của thời gian trước so với trạng thái cân bằng dài hạn, lỗi , ảnh hưởng đến động lực học ngắn hạn của nó. Do đó, các ECM trực tiếp ước tính tốc độ mà một biến phụ thuộc trở về trạng thái cân bằng sau khi thay đổi các biến khác.
….
DỮ LIỆU THANG ĐO
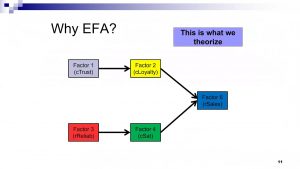
Mô hình EFA
Trong thống kê đa biến , phân tích nhân tố khám phá ( EFA ) là một phương pháp thống kê được sử dụng để khám phá cấu trúc cơ bản của một tập hợp các biến tương đối lớn . EFA là một kỹ thuật trong phân tích nhân tố với mục tiêu bao quát là xác định mối quan hệ cơ bản giữa các biến đo. Nó thường được các nhà nghiên cứu sử dụng khi phát triển thang đo ( thang đo là tập hợp các câu hỏi được sử dụng để đo lường một chủ đề nghiên cứu cụ thể) và phục vụ để xác định một tập hợp các cấu trúc tiềm ẩn bên dưới pin của các biến đo. Nó nên được sử dụng khi nhà nghiên cứu không có tiên nghiệmgiả thuyết về các yếu tố hoặc mô hình của các biến đo. Các biến được đo là bất kỳ một trong số các thuộc tính của những người có thể được quan sát và đo lường. Ví dụ về các biến đo có thể là chiều cao vật lý, cân nặng và nhịp tim của con người. Thông thường, các nhà nghiên cứu sẽ có số lượng lớn các biến đo lường, được cho là có liên quan đến một số lượng nhỏ hơn các yếu tố “không quan sát được”. Các nhà nghiên cứu phải xem xét cẩn thận số lượng các biến đo được đưa vào phân tích. quy trình EFA chính xác hơn khi mỗi yếu tố được biểu thị bằng nhiều biến đo được phân tích.
Mô hình CFA
Trong thống kê , phân tích nhân tố xác nhận ( CFA ) là một hình thức phân tích nhân tố đặc biệt , thường được sử dụng nhất trong nghiên cứu xã hội. Nó được sử dụng để kiểm tra xem các biện pháp của một công trình có phù hợp với sự hiểu biết của nhà nghiên cứu về bản chất của công trình đó (hoặc yếu tố) hay không. Như vậy, mục tiêu của phân tích nhân tố xác nhận là kiểm tra xem dữ liệu có phù hợp với mô hình đo lường giả thuyết hay không. Mô hình giả thuyết này dựa trên lý thuyết và / hoặc nghiên cứu phân tích trước đó. CFA được phát triển đầu tiên bởi Jöreskog và đã xây dựng và thay thế các phương pháp phân tích hiệu lực xây dựng cũ hơnchẳng hạn như Ma trận MTMM như được mô tả trong Campbell & Fiske (1959).
Mô hình SEM
Mô hình phương trình cấu trúc ( SEM ) là một dạng mô hình nhân quả bao gồm một tập hợp đa dạng các mô hình toán học, thuật toán máy tính và phương pháp thống kê phù hợp với các mạng của các cấu trúc với dữ liệu. SEM bao gồm phân tích khẳng định yếu tố , phân tích tổng hợp khẳng định , phân tích con đường , một phần ít nhất người mẫu ô vuông con đường , và mô hình tăng trưởng tiềm ẩn . Không nên nhầm lẫn khái niệm này với khái niệm liên quan của các mô hình cấu trúc trong kinh tế lượng , cũng như với các mô hình cấu trúc trong kinh tế học. Các mô hình phương trình cấu trúc thường được sử dụng để đánh giá các cấu trúc ‘tiềm ẩn’ không quan sát được. Họ thường gọi một mô hình đo lường xác định các biến tiềm ẩn bằng cách sử dụng một hoặc nhiều biến quan sát và mô hình cấu trúc áp đặt mối quan hệ giữa các biến tiềm ẩn. Liên kết giữa các cấu trúc của mô hình phương trình cấu trúc có thể được ước tính bằng các phương trình hồi quy độc lập hoặc thông qua các phương pháp liên quan nhiều hơn như các phương pháp được sử dụng trong LISREL.
…..
SO SÁNH DỮ LIỆU
Trong tên bài viết chúng tôi dùng ” danh sách các mô hình định lượng thông dụng”, nhưng chúng vẫn tôi đưa vào các kiểm định so sánh đơn giản của kinh tế lượng; Tuy là những kiểm định có các lịch sử lâu đời, nhưng hiện tại nó vẫn còn giữ nguyên giá trị của nó, rất nhiều bài báo khoa học hay làm nghiên cứu sinh vẫn sử dụng những kiểm định ” lâu đời” này.
T Test
Anova
Chi2
…..
Trên đây là tổng hợp những mô hình định lượng thông dụng, ngoài ra còn rất nhiều mô hình khác, đã và đang được tạo ra hàng ngày, nếu các bạn làm nghiên cứu khoa học thì nên ứng dụng mô hình nào phù hợp với nghiên cứu của mình nhất, khi bạn làm thạc sĩ thì nên sử dụng các mô hình định lượng thông dụng, nhưng khi cần làm nghiên cứu sinh chúng ta nên phối hợp nhiều mô hinh định lượng với nhau hay sử dụng mô hình định lượng mới, để có những cái mới trong bài nghiên cứu khoa học của mình.