Hiệu chỉnh data PLS-SEM và Chỉnh sửa số liệu SmartPLS nhanh nhất, đối với mô hình plssem thì chúng ta thường xuyên gặp phải nhiều kiểm định rắc rối mà khó có dữ liệu có thể đạt được, vì vậy chúng ta cần xử lý data cho tốt để cho ra kết quả tốt hơn trong quá trình chạy hồi quy bình phương nhỏ nhất từng phần cấu trúc tuyến tính trên phần mềm SmartPLS.
HIỆU CHỈNH DATA PLS-SEM
Chỉnh Sửa Số Liệu SmartPLS
Tại sao phải cần hiệu chỉnh data
Trong mô hình hồi quy cấu trúc tuyến tính pls có rất nhiều kiểm định, kiểm định chất lượng thang đo Cronback’s Alpha > 0.7, Đa cộng tuyến của bộ dữ liệu VIF < 5, Đánh giá về sự hội tụ AVE, CR >0.5, đặc biệt là giá trị riêng biệt HTMT < 0.9 … Đây là những giá trị đầu vào, còn đầu ra nữa cũng không hề dễ dàng gì ? Như hệ số Outer Loading > 0.7, RSMR < 0.8, NFI > 0.9 …và hệ số tác động phải có ý nghĩa thống kê.
Với rất nhiều kiểm định như thế, để có được bộ dữ liệu tốt thì quả thật không dễ, nên trong quá trình nghiên cứu chúng ta gặp phải là thường xuyên.
Nếu bộ dữ liệu của các bạn đã có vấn đề cần hỗ trợ chỉnh sửa data các bạn đừng ngần ngại hãy liên hệ ngay với chúng tôi, để được tư vấn và giải quyết triệt để.
Trong bài này chúng tôi sẽ nói về vài sai phạm của mô hình hồi quy cấu trúc tuyến tình bình phương nhỏ nhất từng phần mà các bạn thường hay gặp phải.
Kiểm định giá trị riêng biệt HTMT
Đây là một kiểm định rất quan trọng mà trong mô hình khám phá nhân tố đã bỏ qua, và cũng được rất nhiều nghiên cứu bỏ qua, vì nó rất dễ bị sai phạm. Đó là kiểm định Heterotrait-monotrait Ratio of Correlations (HTMT), trong kiểm định này yêu cầu các giá trị phải < 0.9 để có tính riêng biệt.
Henseler, Ringle và Sarstedt (2015) cho thấy bằng một nghiên cứu mô phỏng rằng những cách tiếp cận này không phát hiện một cách đáng tin cậy việc thiếu giá trị phân biệt trong các tình huống nghiên cứu thông thường. Do đó, các tác giả này đề xuất một cách tiếp cận thay thế, dựa trên ma trận multitrait-multimethod, để đánh giá tính hợp lệ phân biệt: tỷ lệ tương quan heterotrait-monotrait (HTMT) .
Henseler, Ringle và Sarstedt (2015) chứng minh hiệu suất vượt trội của phương pháp này bằng nghiên cứu mô phỏng Monte Carlo, trong đó họ so sánh phương pháp tiếp cận mới với tiêu chí Fornell-Larcker và việc đánh giá tải chéo (một phần). Cuối cùng, họ cung cấp các hướng dẫn về cách xử lý các vấn đề hợp lệ phân biệt trong mô hình phương trình cấu trúc dựa trên phương sai.
Xem Henseler, Ringle và Sarstedt (2015) để biết giải thích chi tiết về tiêu chí HTMT để đánh giá tính hợp lệ phân biệt trong mô hình phương trình cấu trúc dựa trên phương sai.
Giá trị hội tụ AVE
Trong thống kê ( lý thuyết kiểm định cổ điển ), phương sai trung bình trích xuất (average variance extracted: AVE) là một phép đo lượng phương sai được một cấu trúc thu thập được liên quan đến lượng phương sai do sai số đo; Giá trị này yều cầu phải > 0.5 để có giá trị hội tụ.
Các chỉ số rho_A và CR thường tương quan mật thiết với AVE
Đa cộng tuyến dữ liệu
Một nghiên cứu định lượng thường được nghiên cứu rất kỹ càng, nhưng không hiểu sao mô hình EFA và CB-SEM thì tôi thấy rất ít người kiểm tra dữ liệu có bị đa cộng tuyến không? Nhưng rất may trong phần mềm SmartPLS nó mặc định là có luôn rồi.
Đây là một kiểm định cơ bản, nên cũng không có gì phải bàn nhiều, ai cũng biết VIF < 5 thì không bị đa cộng tuyến.
Chỉ số NFI
Dữ liệu yêu cầu NFI > 0.9 ( Nếu ra kết quả này thì bạn không cần chỉnh sửa số liệu nữa)
Một trong những thước đo phù hợp đầu tiên được đề xuất trong tài liệu SEM là chỉ số phù hợp được định mức bởi Bentler và Bonett (1980). Nó tính toán giá trị Chi² của mô hình được đề xuất và so sánh nó với một điểm chuẩn có ý nghĩa. Vì bản thân giá trị Chi² của mô hình được đề xuất không cung cấp đủ thông tin để đánh giá sự phù hợp của mô hình, NFI sử dụng giá trị Chi² từ mô hình rỗng, làm thước đo. Tuy nhiên, tài liệu không giải thích giá trị PLS-SEM Chi² khác với giá trị CB-SEM như thế nào.
Sau đó, NFI được định nghĩa là 1 trừ đi giá trị Chi² của mô hình được đề xuất chia cho các giá trị Chi² của mô hình rỗng. Do đó, NFI dẫn đến các giá trị trong khoảng từ 0 đến 1. NFI càng gần 1 thì mức độ phù hợp càng tốt. Giá trị NFI trên 0,9 thường thể hiện sự phù hợp có thể chấp nhận được. Lohmöller (1989) cung cấp thông tin chi tiết về tính toán NFI của các mô hình đường dẫn PLS. Tuy nhiên, đối với người dùng đã áp dụng, những giải thích này khá khó hiểu.
NFI đại diện cho một thước đo phù hợp gia tăng. Như vậy, một nhược điểm lớn là nó không phạt về độ phức tạp của mô hình. Càng nhiều tham số trong mô hình, kết quả NFI càng lớn (tức là tốt hơn). Chính vì lý do đó mà biện pháp này không được khuyến nghị, mà là các lựa chọn thay thế như chỉ số phù hợp không theo quy chuẩn (NNFI) hoặc chỉ số Tucker-Lewis, xử phạt các giá trị Chi² theo bậc tự do (df). Lohmöller (1989) đề xuất tính toán NNFI của các mô hình đường dẫn PLS. Tuy nhiên, NNFI vẫn chưa được triển khai trong SmartPLS.
Trên đây chúng tôi liệt kê ra 4 chỉ tiêu thường hay bị lỗi nhất, còn rất nhiều sai phạm cũng xảy ra nhưng không phải thường xuyên, mỗi nghiên cứu sẽ có mỗi lỗi khác nhau, không có gì là chắc chắn cả, nếu bạn bị sai phạm thì phải xử lý làm đẹp dữ liệu lại thôi.
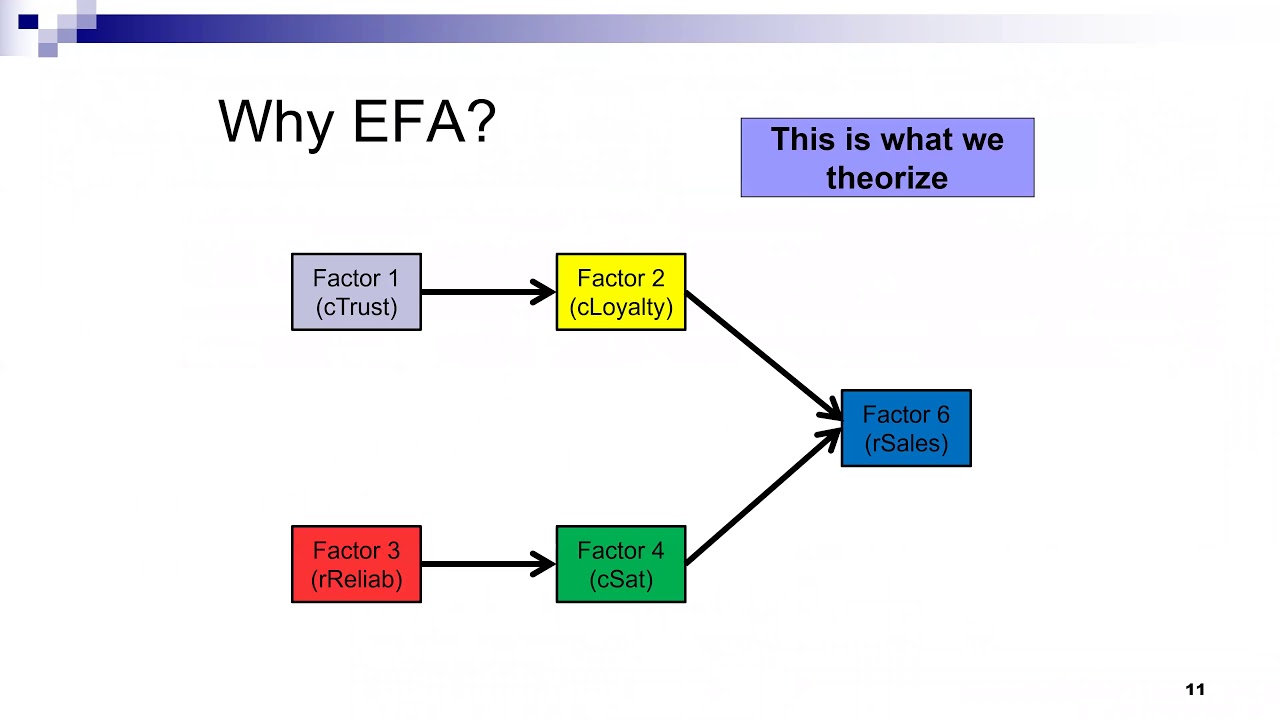
Ví dụ mô hình cấu trúc tuyến tính
Một mô hình giả định cho thấy rằng trí thông minh (được đo bằng bốn câu hỏi) có thể dự đoán kết quả học tập (được đo bằng SAT, ACT và điểm trung bình trung học) được thể hiện trong Hình 1. Khái niệm trí thông minh của con người không thể được đo lường trực tiếp theo cách mà một có thể đo chiều cao hoặc cân nặng. Thay vào đó, các nhà nghiên cứu có lý thuyết và khái niệm về trí thông minh, sau đó thiết kế các công cụ đo lường như bảng câu hỏi hoặc bài kiểm tra cung cấp cho họ nhiều chỉ số về trí thông minh. Các chỉ số này sau đó được kết hợp trong một mô hình để tạo ra một cách đo lường trí thông minh hợp lý dưới dạng một biến tiềm ẩn (vòng tròn cho trí thông minh trong Hình 1) từ các chỉ số (hộp vuông với tỷ lệ 1-4 trong Hình 1).
Trong biểu đồ SEM, các biến tiềm ẩn thường được hiển thị dưới dạng hình bầu dục và biến quan sát là hình chữ nhật. Sơ đồ trên cho thấy lỗi (e) ảnh hưởng như thế nào đến từng câu hỏi trí thông minh và điểm SAT, ACT và GPA, nhưng không ảnh hưởng đến các biến tiềm ẩn. Khi áp dụng mô hình này cho dữ liệu quan sát được tạo ra từ các công cụ, nhà nghiên cứu có thể khôi phục thước đo về trí thông minh và học thuật cho mỗi cá nhân được quan sát với các công cụ với một biên độ sai số được áp dụng bởi các công cụ. Sau đó, nhà nghiên cứu có thể sử dụng trí thông minh để kiểm tra một giả thuyết, chẳng hạn như trí thông minh gây ra kết quả học tập (là một biến tiềm ẩn khác trong Hình 1) được xác định bằng một mô hình đường dẫn vẽ một mũi tên từ trí thông minh đến hiệu suất.
Một ưu điểm lớn của SEM là tất cả các phép đo và kiểm tra này xảy ra đồng thời trong một quy trình ước lượng thống kê, trong đó các sai số trên toàn mô hình được tính toán bằng cách sử dụng tất cả thông tin từ mô hình. Điều này có nghĩa là các sai số chính xác hơn nếu một nhà nghiên cứu tính toán từng phần của mô hình một cách riêng biệt.
Tóm lại, nếu bạn gặp khó khăn trong bộ data sơ cấp thì các bạn cần dịch vụ chỉnh sửa số liệu ngay, không có bộ data nào mà khi điều tra phiếu về có thể đạt được kết quả output SmartPLS là tốt cả.